离散数学全过程反馈混合式教学研究

0 引言

面对科技革命与产业变革的快速发展，《中国教育现代化2035》提出构建学习型社会，满足因材施教与知行合一的需求。智能化环境和信息技术成为教学支撑，教育信息化对教学形式起到重塑的作用，对建构式学习思维培养起到推动作用［1-2］。目前已有教育信息化相关研究，对我国教育发展历程和将来发展形式进行探讨，研究影响学生问题解决能力培养和主动学习的因素［3-4］；发现线上线下结合的教学方式能同时发挥信息技术与面对面教学的优势，有助于提升学生的实际学习水平，成为重要的教学发展方向［5-6］；分析翻转课堂以及在线学习对学生主动学习意愿的影响和提升策略等。研究表明，教师采用线上线下相结合的教学方式以及讨论与实践等教学方法能够有效提升工科生的学习水平和主动性。

1 混合教学中全过程数据反馈现状分析

对于线上线下相结合的混合式教学方式而言，及时、有效的教学反馈是保障教学目标顺利实施的关键［7］。通过师生反馈互动构建“过程式+沉浸式”的双重路径，有助于实现线上与线下教学的实质等效。姚佳佳等［8］研究同伴对话反馈对大学生课堂深度学习的影响；李怡然等［9］根据对学生学习状态的评估反馈，提出基于云控制的闭环OBE 模式。然而，如何实现及时、有效的线上线下全过程反馈是实际教学亟需提升的短板，目前尚缺少对具体反馈机制的深入研究和过程描述。

新工科建设和双一流建设要求在教学中实现学生高阶学习与实践能力培养，强化学生批判性学习和认知结构融入，提升知识迁移、分析和解决问题的能力。因此，需要对新工科建设进行深入分析，以推进学生的深层次、高层次学习［10］。离散数学作为计算机科学与技术、人工智能、大数据、网络安全等众多新工科专业的核心基础课或必修课，侧重培养学生严谨、规范的表述方式，提升分析、解决问题的能力及抽象思维。马慧等［11］分析了离散数学的实例化概念教学法；王晓华等［12］研究了离散数学实践教学体系；苏庆等［13］进行了新工科形式下的离散数学课程改革探索；徐德智等［14］基于CASE 和探索式教学手段，实现学生对离散数学的主动学习。此外，在教学中融入科研训练［15］、研究翻转课堂实践［16］、侧重离散数学的计算思维培养［17］，都是当前涌现的离散数学教学改革方式。

为了推进学生深入学习，需要注重学生的主动学习，促进学生高阶思维的发展。在混合教学中，通过线上线下相结合的方式，充分发挥教师与学生的积极性和主动性。目前已有研究分析了混合教学环境中学习投入影响机制和教学系统化设计模式构建［18-19］。为保障教学质量，李海东等［20］构建了线上线下质量评价流程模型和指标体系；孙传猛等［21］基于目标导向的教育理念（OBE），将工程教育认证标准贯穿始终，助力学生主动学习。线上线下混合式教学需要发挥学生的主动性，但目前教学设计与实施过程缺少对于离散数学以及抽象课程学习的针对性。如何结合课程的抽象特点和学生学习的具体困难，设计全过程的高效反馈强化机制，目前还没有深入的研究成果与系统论述。

本文基于教学数据和全过程反馈实现混合式学习策略设计，横跨课程内外与校内外，围绕离散数学学习与教学反馈难点、教学全过程数据构成与反馈、基于问题解决的深入讨论3 个方面展开论述，并通过实施效果和课程数据分析进行验证。

2 离散数学学习与教学反馈难点

以学生为中心的教学过程需要实现学生价值观、知识、能力等核心素养的提升，通过离散数学的学习，学生在课程结束时可以掌握数理逻辑、集合论、代数结构、图论等知识体系，建立该课程与后续课程的联系，提升计算思维。

离散数学课程具有概念定理多、证明要求高、抽象性强的特点。面对抽象的离散数学，学生会遇到各类困难与困惑。通过抽样调查和学习过程情况分析，可将学生面临的学习困难总结如下：①看着会做，一做就错；②惧怕复杂符号和抽象理论；③难以掌握证明技巧；④抽象理论无法联系实际问题。

当前教学反馈的难点包括学生和教师两个方面。在离散数学学习过程中，学生与教师的联系不够紧密，闭环控制效果不够显著；教师多基于主观判断进行教学决策，教学数据对教学的促进作用不够精确。

对学生而言，由于理论的抽象性和强关联性，很难说清哪些概念和环节理解不够深入或存在偏差，课前预习、课堂学习、课后复习、课外拓展的效果不清晰，难以有针对性地进行提升。学生缺少对课程整体情况的把握，多限于教师布置的课后作业，难以深入参与课程。对任课教师而言，很多课程教学多侧重于一次或一章节作业的批改与讲评，对学生学习状态的整体发展缺少分析，教学决策缺少数据支持。因此，如何构建全面的教学数据采集分析方法，通过全过程数据反馈促进师生闭环，是当前离散数学教学的难点。

3 教学全过程数据构成与反馈

根据教育学理论，学生深度参与教学过程可以有效调动学习的主动性。教学内容、频次、强度的连接能够影响学习感受，创造有信任感和精神安全感的学习氛围，提高学生对教学过程的参与度和掌控感等，以此提升学习效果。离散数学课程全过程反馈形式如图1 所示，全过程数据采集、分析和反馈流程如图2 所示。采用线上线下结合、教材内外结合、校内外结合的方式，可促使学生深度学习，有效提升学生学习的主动性。

如表1 所示，离散数学教学过程中设置了涵盖形成性评价和总结性评价的综合评价方式，全过程与全方位地反馈学生学习状态，有效促进学生线上线下主动学习。

如表2 所示，对离散数学全过程练习和活动进行分析，通过设置参与形式，引导学生参与习题库建设、课程讨论、小组报告等主动学习活动。通过综合练习、学生出题、师生讨论、生生讨论等混合式教学方法，倡导学生动手—动脑—动口相结合，实现主动学习。

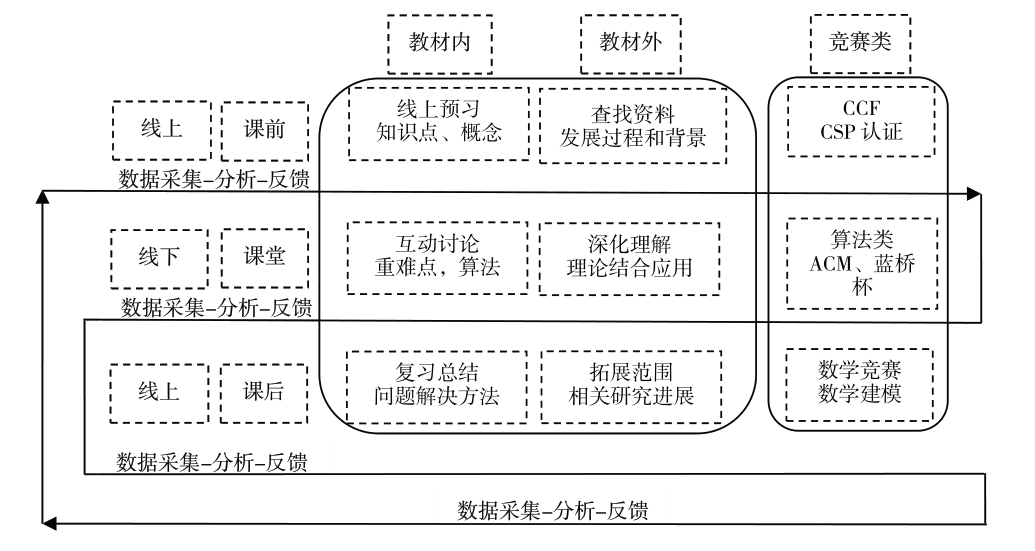
Fig.1 Teaching feedback of discrete mathematics based on the whole process data
图1 基于学习全过程数据的离散数学教学反馈

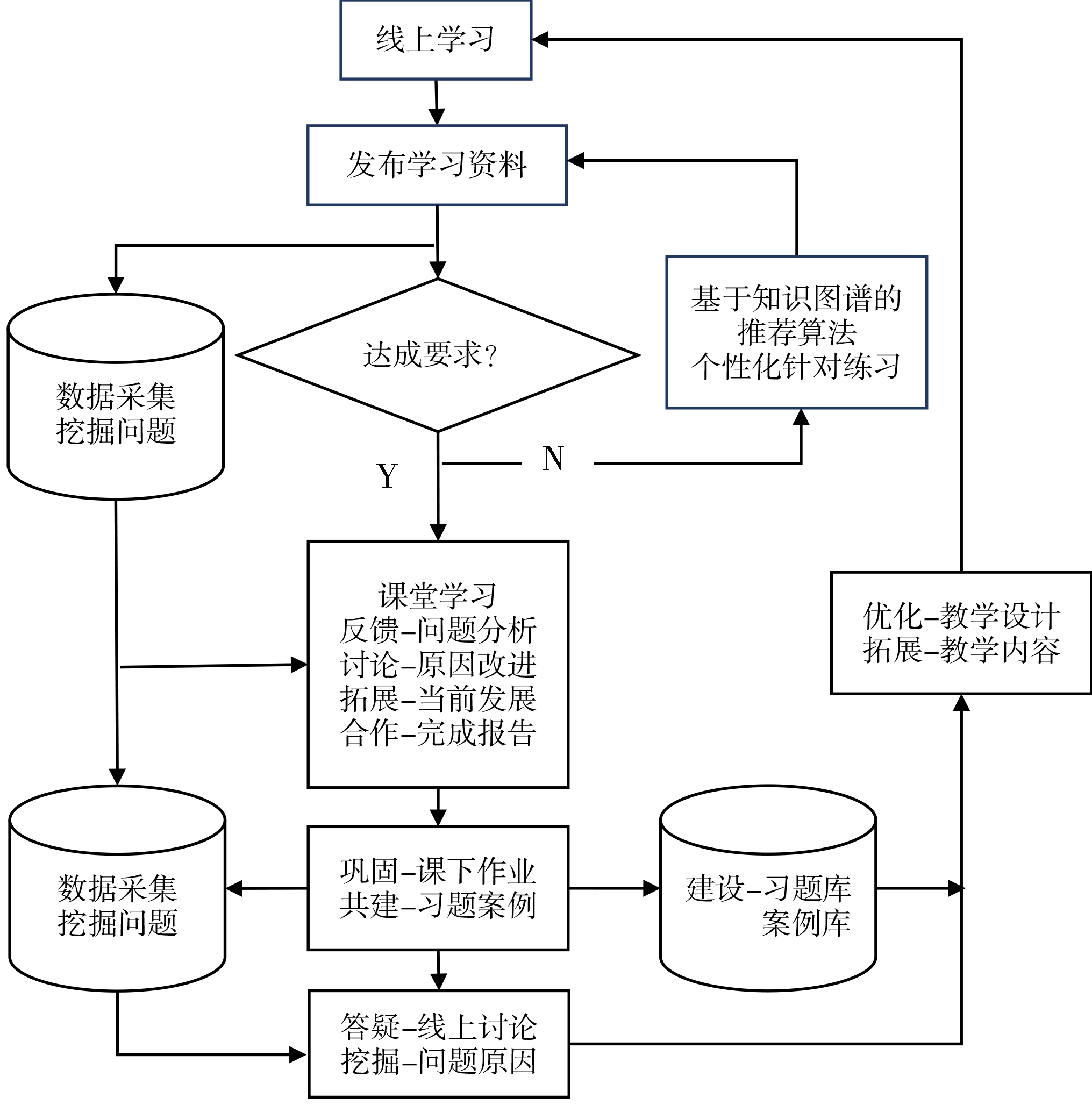
Fig.2 Components of teaching feedback based on the whole learning process
图2 基于学习全过程的教学反馈构成

4 基于问题解决的深入讨论

不断挖掘课程脉络与知识点，通过问题解决的方式进行课程设计。学生思考需要解决哪些问题，怎么解决这些问题？以问题驱动教学，学生自发思考课程的知识体系结构，不断激发学习兴趣。鼓励学生成为主动的建设者，而不仅仅是被动的学习者。

对于科研和工程而言，解决问题的开端是问题建模，对于一个具体实际问题给出合适的模型是有难度的，复杂问题更是对理论与实际的结合提出更高要求。在离散数学的教学中让学生转换角色，增强学生提出问题的主动性，进而可以提升学生解决问题的能力。

Table 1 Form，content，and assessments of whole-process feedback
表1 学习全过程反馈形式、内容与考核方法

Table 2 Comparison of different exercises and teaching activities
表2 不同练习与活动特点对比

练习、讲解、讨论的混合式学习过程，有利于学生及时掌握重难点问题，激发学生独立思考的能力，积极的课堂讨论是水到渠成的结果。本课程设置如下3 类讨论问题：①课前预设。分析课程重难点，针对易错点设置讨论问题；②课堂反馈。通过练习及时了解学生的学习情况，对疑难问题及时讨论；③课后拓展。提供与课程相关的课后拓展材料，并结合课程学习内容，通过在线学习平台进行讨论，学生自己分析如何将理论与实践相结合。

创造充满信任感和精神安全的学习环境，能够促使学生主动表达观点。既表扬回答精彩的学生，也鼓励回答错误的学生。错误的答案通常反映出学生的共同问题，教师作出及时反馈与分析，从而促进学生的共同进步。

实例1 哥尼斯堡七桥问题的模型化方式讨论。

作为图论和拓扑学的起源，欧拉对哥尼斯堡七桥问题给出了图模型，如图3 所示，并给出最终解决方案。在引言部分，如果直接给出该问题的图模型，那么学生只是被动接收，对模型感受并不深。因此，提出讨论问题：能用什么数学工具来描述七桥问题？学生进行思考和讨论后，会发现用传统数学函数来描述七桥问题是很难实现的，如果借用已经学过的二元关系中的关系图，可以直观地表述此问题。与学生共同分析之后，给出欧拉的图模型作为对照，使学生对结点和边的概念有更深刻的理解，也理解了具体问题的数学建模需要通过分析问题的实际特点得到。

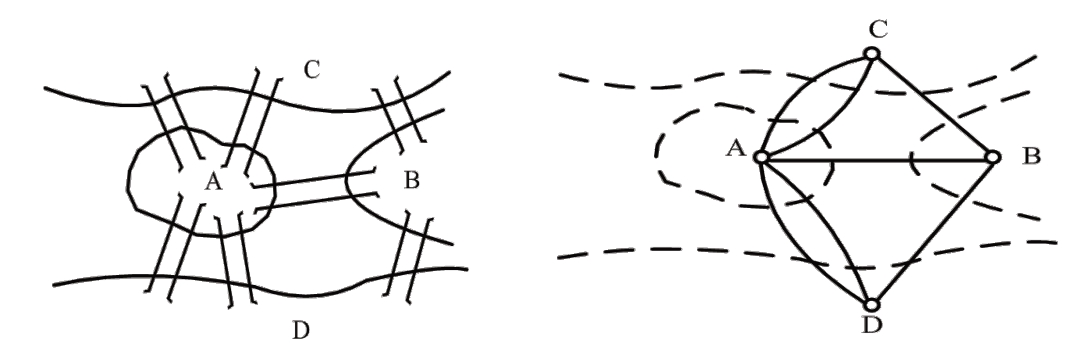
Fig.3 Königsberg seven bridge problem
图 3 格尼斯堡七桥问题

实例2 n元关系的延展思考。

（1）课前预设问题：之前的课程学习和生活中有哪些n元关系？什么是n 元关系？通过什么方式表达n 元关系？关系数据库与n元关系有什么关联？

（2）课堂反馈问题：n 元关系运算与集合运算有什么区别？n 元关系运算和关系数据库操作有什么区别与联系？n元关系与函数存在哪些异同？

（3）课后拓展问题：当前国产数据库中，华为Gauss DB与蚂蚁金服的Ocean DB 是典型代表，查询相关产业需求与发展趋势，以及大数据中是否用到关系概念？

5 实施效果及数据分析

5.1 学生评教结果

中国海洋大学每学期均组织全体学生对课程进行评教，根据近3 年学校教学质量管理平台的评价结果，离散数学课程团队的平均分为96.92 分，高于学校的平均分（93.99 分）和同类型课程平均分（93.52 分）。教学质量评价的主要调查问题及支持比例如表3 所示，评教结果显示了基于全过程反馈的混合式课程教学的有效性。通过基于问题解决的启发式互动教学，师生实现有效反馈，学生能够积极面对离散数学的高挑战性，并极大地激发了学习兴趣。

5.2 基于专业认证的课程目标达成度分析

设置4 个课程目标，基于工程认证的需求，对课程进行持续改进。①课程目标1。掌握离散数学的基础概念和应用，培养学生独立思考的能力与创新精神，激发学生科技报国的爱国热情；②课程目标2。掌握数理逻辑、集合论与代数结构、图论等理论知识和证明方法及其在实际问题中的应用，构建相对完整的离散数学理论框架；③课程目标3。掌握对实际问题进行数学建模的理论化描述方法，培养学生在理论研究和工程应用中严谨的数学逻辑推理与分析解决问题的能力；④课程目标4。培养学生的团队合作能力和表达能力，通过自行查找资料并分析，提升科技文档的整理能力与语言表达能力。

Table 3 Mainly investigated problems of teaching quality evaluation and support proportion
表3 教学质量评价主要调查问题及支持比例

如表4 所示，根据工程认证进行指标点对应，考察学生的学习过程和课程考核结果，获得4 个课程目标的达成度分析。其中，A5，1、A5，2、A5，3为期末考试成绩，分别对应课程目标1、课程目标2 和课程目标3 的得分，A5，1+A5，2+A5，3=60。2021 年离散数学的课程目标达成度如图4所示。

Table 4 Complementation degree of course goals based on the learning process and test results
表4 基于学习过程与考核结果的课程目标达成度

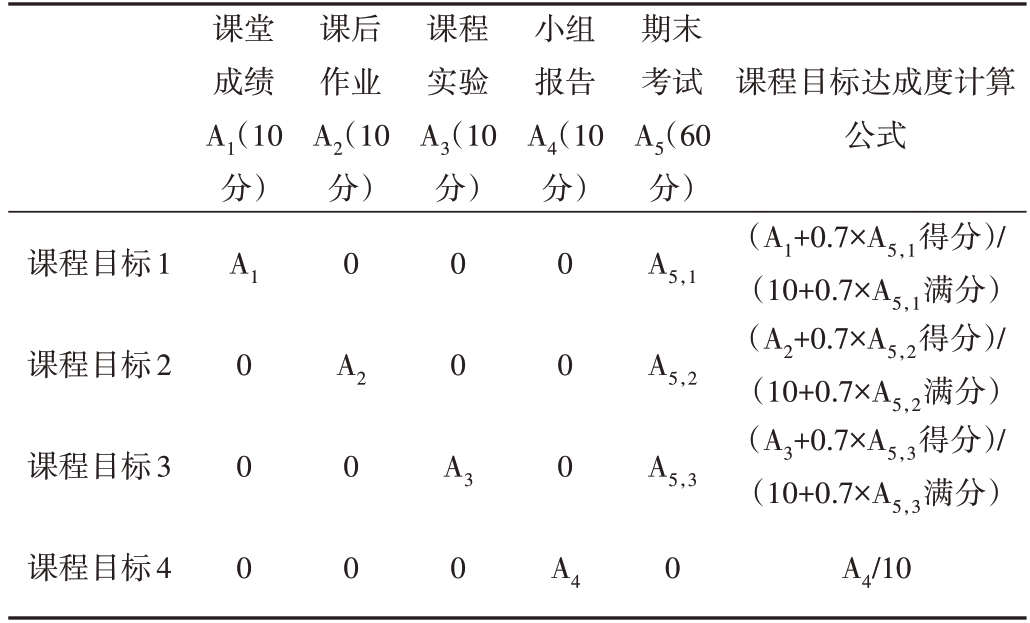
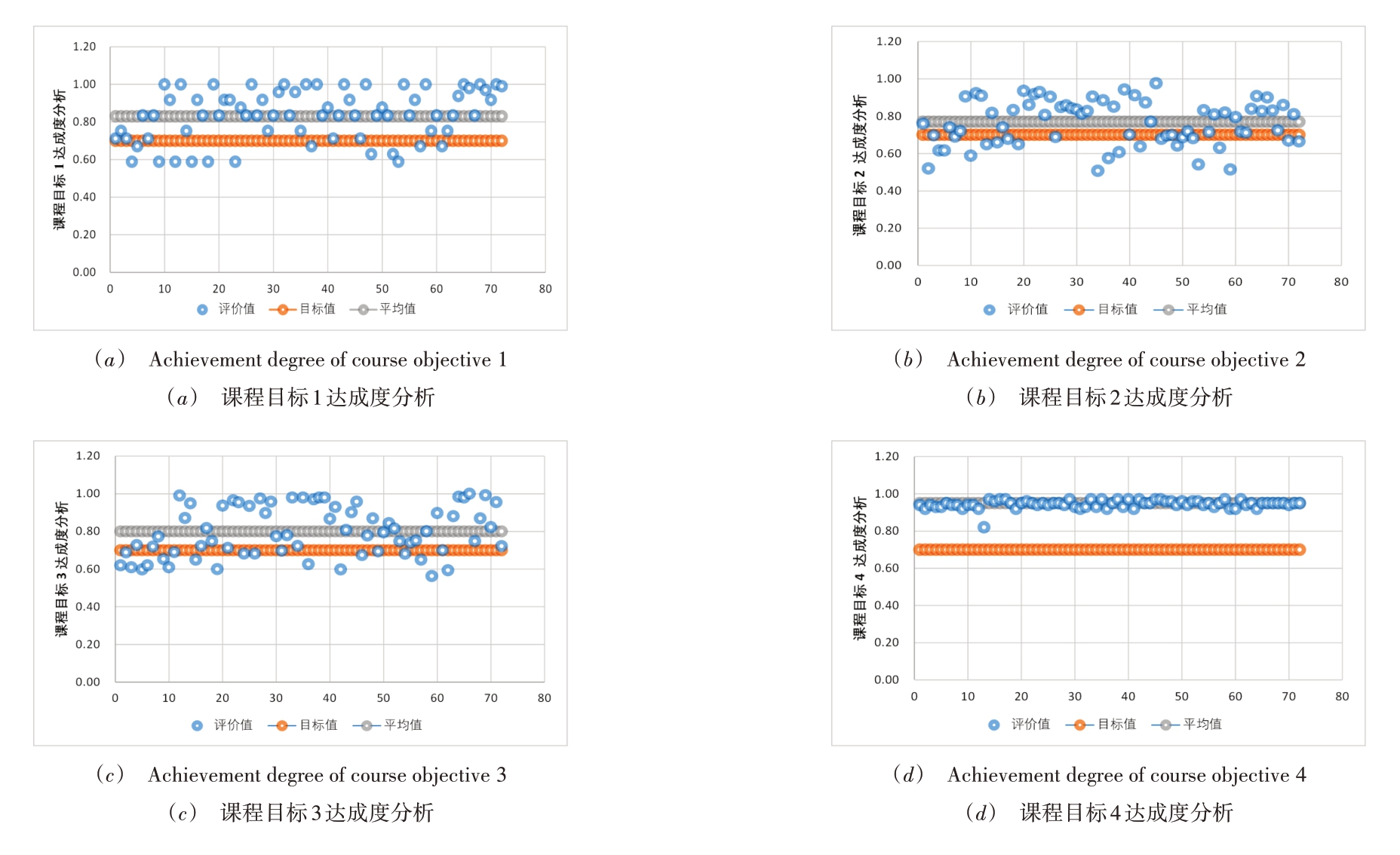
Fig.4 Analysis of course objective achievement degree
图 4 课程目标达成度分析

设置各课程目标达成度为0.7，所有课程目标均达到评价要求。其中，课程目标1 达成度为0.83，课程目标2 达成度为0.77，课程目标3 达成度为0.80，课程目标4 达成度为0.94。学生在科技报国责任感、创新精神和小组合作方面的目标达成度较高，从而进一步带动了在课程实验、竞赛、认证考试等其他方面的学习与表现。

5.3 小组报告和课程实验带动CSP认证及课外竞赛成绩

在抽象理论学习中设置灵活的课程实验，为学生参加CCF-CSP 认证、算法编程类竞赛、数学竞赛等打下良好的算法与程序基础。近年来中国海洋大学计算机专业学生参加CCF-CSP 认证的成绩逐年提高，以150 分为认证通过线，每年超过200分的考生人数占比从17%提升到58%。

通过基于全过程数据反馈的课程改革，有效提升了学生的算法分析和实现能力以及信息安全的数理基础与迁移拓展能力。近5 年来，学生成绩优异，在国内外竞赛中多次获得“高教社杯”全国大学生数学建模竞赛一等奖、全国大学生信息安全竞赛一等奖、ACM-ICPC 国际大学生程序设计竞赛亚洲区域赛金牌等。

6 结语

本文基于线上线下教学和全过程考核反馈，提升学生的课程参与程度，实现对离散数学的主动学习。针对学生学习过程中存在的学习动力问题和目标疑问、学习细节难点等，从全过程化管理与反馈强化入手，整合校内校外、课内课外、本课程和后续发展的关系，提升学生的学习效果。教学实践证明了该教学方法的有效性，可契合专业认证目标，符合目标导向的教学理念。后续研究将进一步深化对课程数据的自适应管理。

参考文献：

［1］ YANG X W，JIN Z，HU Y J.How initiative learning is possible：retrospect and prospect of teaching reform over the past 70 years since the founding of new China［J］.Journal of the Chinese Society of Education，2019（10）：17-21.

杨小微，金哲，胡雅静.主动学习何以可能：新中国成立70 年教学改革的回眸与前瞻［J］.中国教育学刊，2019（10）：17-21.

［2］ HUANG R H，WANG Y，WANG H H，et al.The new instructional form of the future education：flexible instruction and active learning［J］.Modern Distance Education Research，2020，32（3）：3-14.

黄荣怀，汪燕，王欢欢，等.未来教育之教学新形态：弹性教学与主动学习［J］.现代远程教育研究，2020，32（3）：3-14.

［3］ DING F J.The characteristics of problem-solving skill of engineering undergraduates and its influence factors［J］.China Higher Education Research，2020（5）：17-23.

丁飞己.工科本科生问题解决能力及其影响因素研究［J］.中国高教研究，2020（5）：17-23.

［4］ GAO W，XU S Y.A study of classroom observation and reflection tool for college teachers to promote students' active learning——taking PORTAAL as an example［J］.Research in Teaching，2019，42（5）：15-26.

高巍，徐仕晔.高校教师促进学生主动学习的评价量表研究—以PORTAAL为例［J］.教学研究，2019，42（5）：15-26.

［5］ ZHU G P，YU X J.Active learning promotion strategies based on flipped classrooms［J］.China University Teaching，2018（5）：112-114.

朱桂萍，于歆杰.基于翻转课堂的主动学习促进策略［J］.中国大学教学，2018（5）：112-114.

［6］ WANG S F，HUANG R H.Research on the mechanism and promotion strategy of online active learning intention［J］.Open Education Research，2020，26（5）：99-110.

王绍峰，黄荣怀.在线主动学习意愿的产生机理与提升策略［J］.开放教育研究，2020，26（5）：99-110.

［7］ LIU Y H，SHAN P J，MO F.How can realize “substantial equivalence” between online and off-line teaching［J］.Journal of National Academy of Education Administration，2021（3）：67-75.

刘艳红，单平基，莫凡.线上与线下教学质量“实质等效”何以可能［J］.国家教育行政学院学报，2021（3）：67-75.

［8］ YAO J J，LI Y，CHEN X Y，et al.Research on promotion effect of realtime dialogic peer feedback on college students' deep learning in classroom［J］.e-Education Research，2022，43（1）：113-121.

姚佳佳，李艳，陈新亚，等.基于实时互动的同伴对话反馈对大学生课堂深度学习的促进效果研究［J］.电化教育研究，2022，43（1）：113-121.

［9］ LI Y R，XIA Y Q.Exploration on closed-loop OBE-oriented online courses based on cloud control［J］.Research and Exploration in Laboratory，2021，40（7）：149-153.

李怡然，夏元清.基于云控制的闭环OBE 在线教学模式探索［J］.实验室研究与探索，2021，40（7）：149-153.

［10］ GU P H.Thinking on the development and deepening of new engineering construction［J］.China University Teaching，2019（9）：10-14.顾佩华.新工科建设发展与深化的思考［J］.中国大学教学，2019（9）：10-14.

［11］ MA H，SHENG Y X，XU J L，et al.Enhancing comprehension of concepts via real examples in discrete mathematics［J］.Computer Education，2011（12）：57-59.

马慧，盛艳秀，徐建良，等.离散数学的实例化概念教学法［J］.计算机教育，2011（12）：57-59.

［12］ WANG X H，WANG R G，YANG J，et al.Research on the practical teaching system of professional basic courses with discrete mathematics as the core in the background of new engineering［J］.Computer Education，2018（10）：146-149.

王晓华，汪荣贵，杨娟，等.新工科背景下离散数学为核心的专业基础课程实践教学体系研究［J］.计算机教育，2018（10）：146-149.

［13］ SU Q，LIN H Z，LI Z Y.Exploration of teaching reform of discrete mathematics curriculum under the new engineering situation［J］.Computer Education，2019（1）：25-28，32.

苏庆，林华智，黎展毅.新工科形势下离散数学课程教学改革探索［J］.计算机教育，2019（1）：25-28，32.

［14］ XU D Z，SHI R H，PENG J."Discrete Mathematics" classroom teaching based on active learning［J］.Computer Education，2012（6）：51-53.

徐德智，施荣华，彭军.基于主动学习的“离散数学”课堂教学［J］.计算机教育，2012（6）：51-53.

［15］ WANG Q X，GU X F.Research and teaching of discrete mathematics courses to cultivate undergraduate research literacy［J］.Computer Education，2021（4）：140-142.

王庆先，顾小丰.以研促教的离散数学课程本科生科研素养培养［J］.计算机教育，2021（4）：140-142.

［16］ LIANG D L.An exploration of discrete mathematics flipped classroom teaching practice on the basis of the fusion of online and offline［J］.College Mathematics，2019（35）：45-49.

梁道雷.基于线上+线下融合的离散数学翻转课堂教学实践探究［J］.大学数学，2019（35）：45-49.

［17］ JIA J D，LI W G.Discrete mathematics teaching reform based on computational thinking oriented ability development［J］.Computer Education，2021（9）：152-155.

贾经冬，李卫国.基于计算思维面向能力培养的离散数学教学改革［J］.计算机教育，2021（9）：152-155.

［18］ MA J.Influence mechanism of college students' learning engagement in a blended learning environment：from the perspective of teaching behaviors［J］.Chinese Journal of Distance Education，2020（2）：57-67.

马婧.混合教学环境下大学生学习投入影响机制研究—教学行为的视角［J］.中国远程教育，2020（2）：57-67.

［19］ ZHU Y H.Systematic design and systematic mode construction of blended teaching from the perspective of deep learning［J］.China Educational Technology，2021（11）：77-87.

朱永海.深度学习视角下混合教学系统化设计与体系化模式构建［J］.中国电化教育，2021（11）：77-87.

［20］ LI H D，WU H.Research on blended teaching quality evaluation system based on the whole process：a national online and offline blended firstclass course as an example［J］.China University Teaching，2021（5）：65-71，91.

李海东，吴昊.基于全过程的混合式教学质量评价体系研究—以国家级线上线下混合式一流课程为例［J］.中国大学教学，2021（5）：65-71，91.

［21］ SUN C M，DU H M，LI X，et al.Research on teaching mode of intelligent control course based on OBE and PAD class concept［J］.Research in Higher Education of Engineering，2022（1）：157-162.

孙传猛，杜红棉，李晓，等.融合OBE 与PAD 理念的智能控制课程教学模式研究［J］.高等工程教育研究，2022（1）：157-162.