一个离散数学辅助教学软件的设计与开发

1 引言(Introduction)

离散数学是计算机专业的核心基础课程，通常包括逻辑、证明、集合、关系、函数、组合计数、图论和代数等多个模块。离散数学课程的内容抽象，概念众多，教师希望能有很多可选的例子帮助讲解相关内容，学生也希望有更多的例子帮助理解和做更多的练习，但教材受篇幅所限通常不会提供太多的例题和习题，对于例题的求解过程有时也不会写得非常详细。教师自己想拟出更多例子时，却由于思维的某种局限性，往往拟出的例子与已有例子非常相似，例子的复杂性和代表性都可能不够。因此，一款能够随机生成例子并给出详细求解过程的计算机软件对离散数学课程的教学和学习都会非常有帮助[1]。

离散数学被认为是计算机学科的基础理论之一，其中很多问题都是可以使用计算机程序进行求解的。很多问题的求解算法，例如关系闭包的计算算法(Warshall算法)通常也是离散数学课程的知识内容之一，有些教材也会提供编程练习题[2-3]，因此利用计算机程序求解离散数学问题并展示问题求解过程是帮助学生学习这门课程的一种可行途径。遗憾的是，目前还很缺乏这方面的软件，只有一些零散的离散数学课程中有算法的实现代码展示[4-8]，却不能生成例子并展示详细求解过程。有些通用的大型数学软件或计算代数系统(Computer Algebra System,CAS)，如Maple、Mathematica、Magma等虽然也能用于求解离散数学问题，但不会展示求解过程，或者求解过程需要用户自己使用软件提供的语言编程实现，很难用于离散数学课程例子的自动生成。

我们在编写教材[3]时为构造特有的例子和验证解答的正确性，在前期一些零散演示工具[9]的基础上，使用面向对象方法设计和开发了一个离散数学辅助教学软件——离散数学基础例题演示软件Deedm(Demonstrator for Examples in Elementary Discrete Mathematics)，实现了命题逻辑、集合、关系、函数、组合计数、图论和代数中多个离散数学问题的例子生成和求解过程的展示。学生使用这个软件可更好地理解教材例子并得到教材许多习题的详细解答范本；教师使用这个软件可生成更多例子用于考试或课堂讲解，减轻了教师备课和出卷的工作量。

2 软件功能分析与总体架构(Software function analysis and its architecture)

离散数学基础例题演示软件Deedm的基本功能是离散数学课程中一些问题的例子生成和详细求解过程的展示。我们在参考多本国内外离散数学优秀教材的基础上，确定Deedm至少能对下面的问题生成例子并展示其求解过程：

(1)命题逻辑公式真值表的构造，以及将命题逻辑公式的析取范式或合取范式扩展为等值的主析取范式或主合取范式。

(2)集合的并、交、差、补、对称差和幂集运算，关系和函数的复合运算，关系逆运算，关系性质(自反性、对称性、传递性等)的判断，关系闭包的计算，函数性质(单函数、满函数、双函数)的判断，等价关系等价类和商集的计算，偏序集极大元、极小元、最大元、最小元的确定，偏序集子集上界、下界、上确界和下确界的确定。

(3)组合计数中n元素集合的r排列生成，n元素集合的r组合生成，n元素集合的允许重复的r组合生成，满足指定计数条件的字符串枚举，满足指定整除性质的整数枚举，满足指定条件的不定方程解枚举。

(4)无向图或有向图的遍历，根树的遍历，带权图指定顶点到其他顶点最短路径的计算，带权图最小生成树的确定，给定带权叶子的最优二叉树构造。

(5)给定运算表性质(交换律、结合律、幂等律、分配律、吸收律、单位元、零元、逆元、消去律)的判断，一些特殊有限群(例如n元素集合上的置换群，与m互质的正整数以模m乘为运算构成的U(m)群)的群元素阶、子群、子群陪集、正规子群、商群的计算，一个偏序集是否是格、分配格、有补格或布尔代数的判定。

不难看到，这些已经覆盖常见离散数学教材中绝大多数可使用计算机程序进行求解的问题。为支持这些问题的例子生成和求解过程展示，我们设计了如图1所示的Deedm软件的总体架构。

我们采用面向对象方法[10]设计，图1中每个方块包含一个或多个实体(Entity)，它们之间的箭头表示这些实体间的支持关系，即一个实体在提供某些功能或服务时需要另外模块一些实体的支持，例如命题逻辑公式范式中的实体实现将析取范式或合取范式扩展为主范式的功能，需要命题逻辑公式中实体的支持。

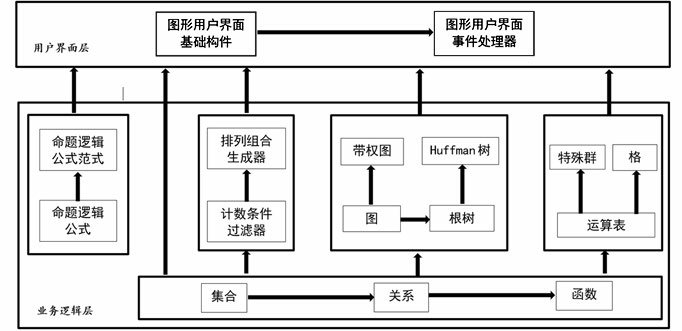
图1 离散数学基础例题演示软件Deedm的总体架构
Fig.1 The software architecture of Deedm

可以看到，Deedm软件总体分为两层，即用户界面层和业务逻辑层。业务逻辑层又分为五个模块，分别支持逻辑、集合关系函数、组合计数、图论和代数中问题的例子生成和求解过程展示。用户界面层的事件处理器使用基础构件中的实体实现与用户交互，并调用业务逻辑层的实体提供的功能完成例子生成和求解过程在图形用户界面上的展示。

3 软件的面向对象设计(Object-oriented design of software)

Deedm软件的设计采用面向对象方法。在梳理离散数学相关知识的基础上，根据面向对象思想，在软件中创建对应离散数学知识内容的实体，根据实体本身的特点(而非根据要实现的功能的需要)设计实体属性和功能，然后通过这些实体之间的交互实现软件需要实现的功能。这种面向对象设计使得软件具有很好的可重用性和可扩充性。

我们选择使用Java语言实现Deedm软件，软件的用户界面层主要是基于JavaSwing组件实现基础构件支持离散数学问题的例子及其求解过程的展示，并基于JavaGUI事件监听机制实现事件处理器捕捉与用户交互过程中的事件，调用业务逻辑层实体提供的服务完成离散数学问题例子的生成和求解。因此下面只对业务逻辑层的设计作更详细的介绍。

业务逻辑层可分为逻辑、集合关系函数、组合计数、图论和代数五个模块，目前逻辑、组合计数、图论和代数这四个模块之间是相互独立的，但是集合关系函数模块的实体支持组合计数、图论和代数这三个模块的实体，因为它们都要用到集合。下面主要以类图的形式介绍这五个模块设计的主要思路。

3.1 逻辑模块的设计

逻辑模块的主要功能是实现命题逻辑公式真值表的构造和将范式扩展为主范式。根据面向对象思想，对应离散数学命题逻辑的基础知识，这一模块的主要实体是命题逻辑公式和命题逻辑公式范式，图2给出了其中主要实体及其关系。

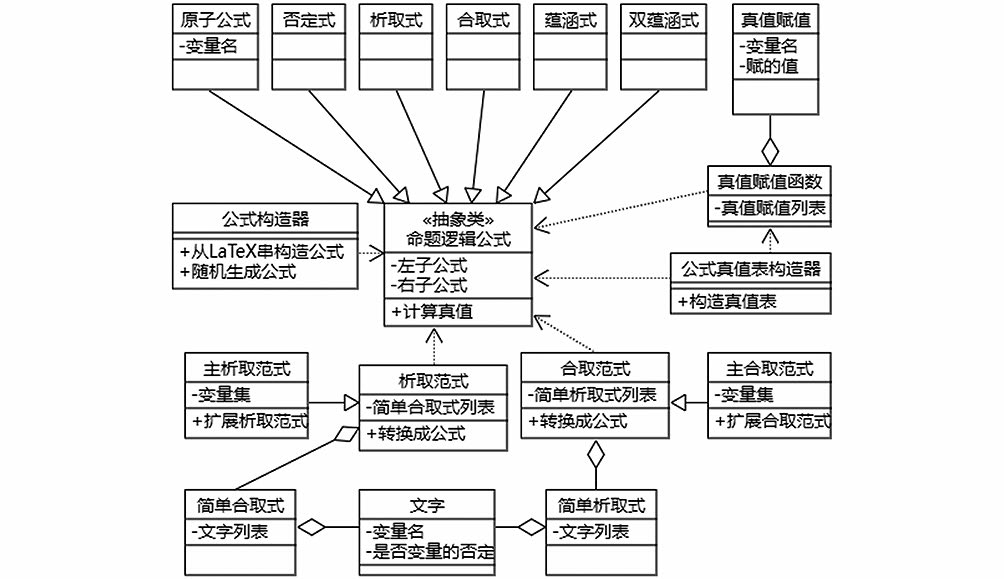
图2 逻辑模块的主要实体(类)及其关系图
Fig.2 Main entities (classes) and their relationship diagram of the logic module

逻辑模块的核心实体是命题逻辑公式(为方便起见以下简称“公式”)，它是一个抽象类，包含一个左子公式和一个右子公式作为它的主要属性，从而公式本身形成了一个二叉树结构，即一个命题逻辑公式实际上存放的是该公式的抽象语法树。基于命题逻辑公式的语法，这个实体派生出原子公式、否定式、析取式、合取式、蕴涵式和双蕴涵式(逻辑等价式)六个实体，它们重定义公式所提供的计算真值的服务。公式真值计算需要真值赋值函数，这是真值赋值的列表，每个真值赋值为一个变量名指定一个真值。公式真值表构造器可以根据指定的真值赋值函数计算公式的真值，也可收集公式出现的所有变量，生成所有可能的真值赋值函数从而构造公式的真值表。构造的结果是一个数据表管理器，它将真值表当作二维表存放。公式构造器使用简单的算符优先分析算法分析一个字符串的语法，并将其转换为命题逻辑公式这个实体的一个实例，这种字符串里支持使用LaTeX命令表示逻辑运算符。公式构造器还支持随机生成一个命题逻辑公式。

对于命题逻辑公式范式，文字包含一个变量名，并有一个布尔变量表明该文字是变量本身还是变量的否定。目前无论是原子公式中的变量还是文字中的变量，都只支持由一个字符表示变量名。简单析取式和简单合取式都是文字的列表，而析取范式是简单合取式的列表，合取范式是简单析取式的列表。析取范式和合取范式都提供服务将它的实例转换为一个命题逻辑公式的实例。主析取范式和主合取范式分别集成析取范式和合取范式，提供服务根据给定的变量集将范式扩展为主范式。

3.2 集合关系函数模块的设计

集合关系函数模块的主要功能是实现集合、关系和函数的运算，关系性质和函数性质的判断。根据面向对象思想，对应离散数学集合、关系和函数部分的基础知识，这一模块的主要实体是集合、关系和函数，图3给出了其中主要实体及其关系。

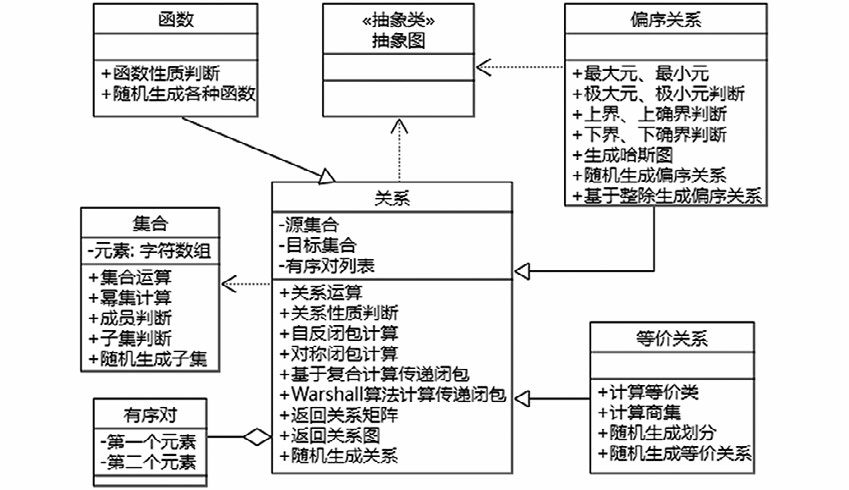
图3 集合关系函数模块的主要实体(类)及其关系图
Fig.3 Main entities (classes) and their relationship diagram of the set-relation-function module

集合关系函数模块的核心实体是集合和关系。目前实现的集合只支持字符或整数作为元素(实际上字符也被看作整数，只是在屏幕显示时作不同处理)。集合实体提供集合并、交、差、对称差、幂集等的计算。关系实体存储有序对的列表，并记录关系的源集合和目标集合。有序对的元素也只能是字符或整数。目前设计的集合实体不能存在任意类型的元素，因此关系实体与集合实体之间没有继承关系，关系实体也提供并、交、差、复合、逆及闭包的计算，并提供对关系性质的判断。函数被看作是一种特殊的关系，因此继承关系的属性和服务，并提供对函数性质的判断。等价关系和偏序关系也都继承关系的属性和服务。等价关系还可计算等价类和商集，偏序关系可返回极大元、极小元等各种元素，并支持绘制哈斯图。关系支持绘制关系图，哈斯图和关系图都是图论模块中抽象图的实例。

3.3 组合计数模块的设计

组合计数模块的主要功能是实现满足各种条件的计数对象枚举，从而可用于验证计数问题求解的正确性。图4给出了其中主要实体及其关系。

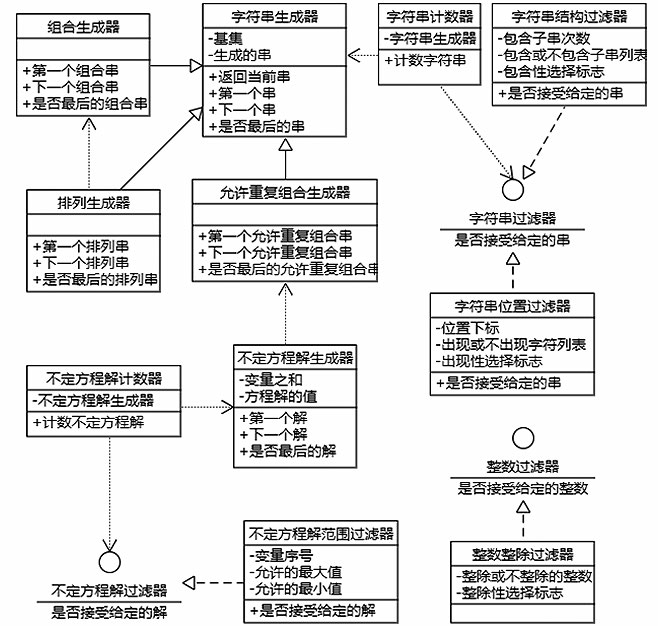
图4 组合计数模块的主要实体(类)及其关系图
Fig.4 Main entities (classes) and their relationship diagram of the combinatorial counting module

采用过滤器模式生成满足条件的计数对象，即将在合适的、有规律范围内生成计数对象和根据计数条件过滤计数对象这两个功能分离，从而具有更好的灵活性和可扩充性。因此，组合计数模块的核心实体分为两大类，一类是生成器，一类是过滤器。生成器中最基本的是字符串生成器，它支持生成某个基集上允许重复字符的所有字符串，排列生成器、组合生成器和允许重复组合生成继承字符串生成器分别生成基集上指定长度的排列(不允许重复)、组合和允许重复的组合。不定方程解生成使用允许重复组合生成器生成不定方程的解。

离散数学基础课程主要关注字符串的计数、基于整数整除性质的整数计数和不定方程解的计数，因此分别设计了三个接口，并分别提供字符串位置过滤器、字符串结构过滤器、整数整除过滤器和不定方程解范围过滤器作为这些接口最基本的实现。过滤器模式的一个优势是通过组合过滤器实现复杂条件的过滤，因此每种过滤器还提供逻辑与关系和逻辑或关系的组合过滤器(限于篇幅，图4没有画出)，以实现条件的组合。

3.4 图论模块的设计

图论模块的主要功能是实现图和树的遍历，并实现带权图最短距离的Dijkstra算法、最小生成树的Kruskal和Prim算法，以及构造最优二叉树的Huffman算法。图5给出了其中主要实体及其关系。

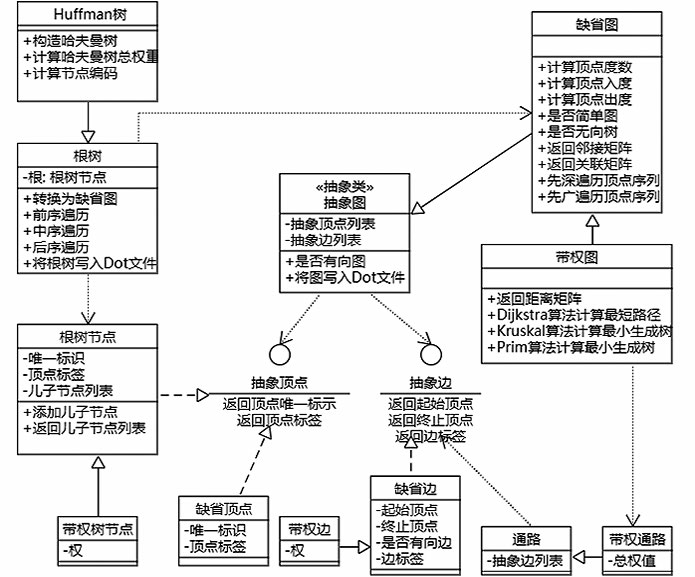
图5 图论模块的主要实体(类)及其关系图
Fig.5 Main entities (classes) and their relationship diagram of the graph theory module

图论模块的一个核心实体是抽象图，它维持一个抽象顶点列表和一个抽象边列表。抽象顶点和抽象边都是接口，实现它们的实体都可作为抽象图的顶点和边。实体缺省图提供了抽象图的一个具体实现，它实际使用的顶点和边是实体缺省顶点和缺省边的实例，提供计算顶点度数、返回图的邻接矩阵和关联矩阵等服务，并支持对图的先深遍历和先广遍历。带权图继承缺省图，使用带权边的实例作为它的边，实现Dijkstra算法、Kruskal算法和Prim算法。

图论模块的另一个核心实体是根树，它维持一个根树节点作为它的根，根树节点维持一个根树节点列表作为它的儿子节点列表。根树提供树的前序、中序和后序遍历。根树没有继承抽象图这个实体，但可转换为缺省图。Huffman树继承根树，以带权树节点作为它的节点，并实现Huffman算法。

3.5 代数模块的设计

代数模块的主要功能是判断运算的性质，展示一些特殊群的子群、陪集，以及判断格的性质。图6给出了其中主要实体及其关系。

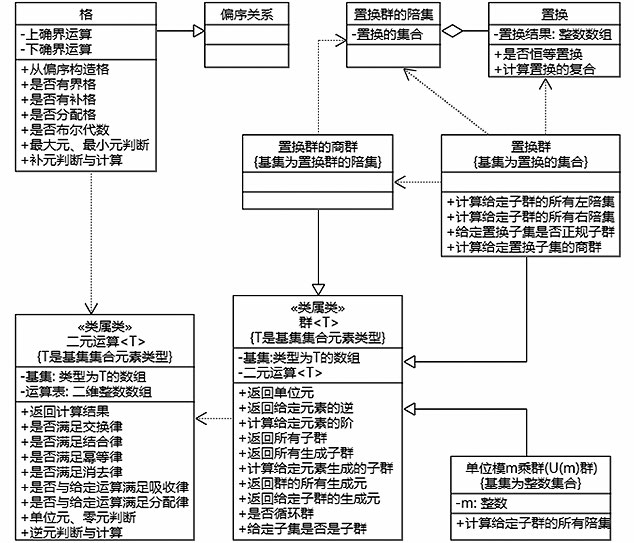
图6 代数模块的主要实体(类)及其关系图
Fig.6 Main entities (classes) and their relationship diagram of the algebra module

代数模块的核心实体是二元运算，它的基集类型是一个类型参数，因此是一个类属类。将二元运算作为类属类是因为置换群、U(m)群和格等不同代数系统的基集元素类型不同，而这些代数系统都有二元运算，都需要二元运算这个实体提供的有关运算性质判断的服务。类似地，群这个实体也是一个类属类，它提供有关群元素的阶，判断子集是否是子群，计算所有子群、所有生成子群，计算子群生成元等服务。单位模m乘群(U(m)群)继承群这个实体，并且将基集元素的类型定为整数，提供计算子群陪集的服务。置换群继承群这个实体，它的基集元素类型是置换。置换是集合{1,2,…,n}上的一个双函数，使用一个整数数组表示置换结果，即数组的第i 个元素记录的是这个双函数作用在整数i的值。置换群这个实体提供计算子群的左右陪集、判断子群是否是正规子群，以及计算给定正规子群的商群等服务。格继承集合关系函数模块中的偏序关系这个实体，并维持两个二元运算，提供判断格的性质，返回最大元、最小元、补元(如果有的话)等服务。

4 软件实现关键技术与运行效果(Key technology of the software implementation and its operation effect)

面向对象的设计使得Deedm软件的结构与离散数学课程的知识结构有很好的对应关系，使得整个软件具有很好的可理解性和可扩充性。Deedm软件使用面向对象语言Java语言实现，在面向对象设计的基础上，实现阶段主要解决的关键问题包括：

(1)如何方便地输入和显示数学符号。很多数学符号，例如逻辑运算符等都不是可从键盘直接输入的符号，它们的显示也不能简单地以字符串的方式显示。对于这个问题，Deedm软件支持用户使用LaTeX命令输入逻辑运算符等数学符号，并使用Java构件库JLaTeXMath解析含有LaTeX命令的字符串并生成符合数学风格排版的图片，从而解决了数学符号的输入和显示问题。

图7展示了命题逻辑公式的输入及其真值表构造的效果，可看到用户使用LaTeX命令，例如\rightarrow等录入逻辑运算符，Deedm软件以图片的形式显示输入的公式以及构造的真值表。

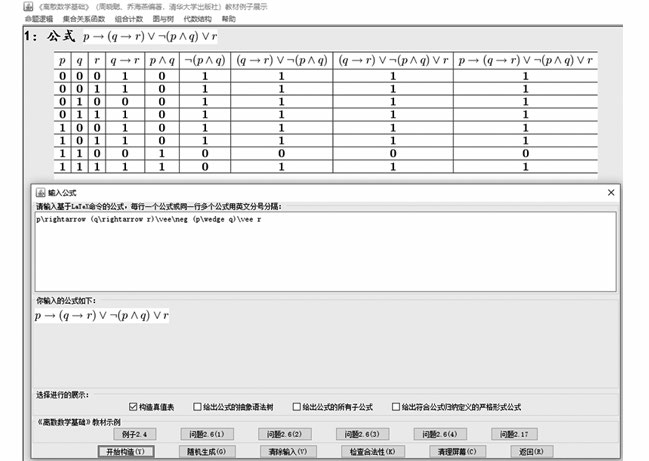
图7 命题逻辑公式的输入及其真值表构造
Fig.7 Input of propositional logic formula and its truth table construction

(2)如何生成离散数学课程中一些问题的例子。促使我们开发Deedm软件的一个动机是希望能针对一些离散数学问题生成例子供教师讲课、测验和学生学习练习使用。为此，Deedm软件的许多实体(类)都实现了随机生成的功能，例如在命题逻辑公式构造器中有随机生成命题逻辑公式的Java方法。图8给出的输入界面也支持命题逻辑公式的随机生成。可以看到，在前文给出主要模块的设计中，很多实体都提供了随机生成的服务。有些离散数学问题的例子生成，如集合、普通关系的生成比较简单，采用随机函数从合适集合随机选取元素即可，但有些问题的例子生成，例如要生成偏序关系、等价关系等，需要设计一些算法才能保证生成的关系是偏序关系或等价关系。

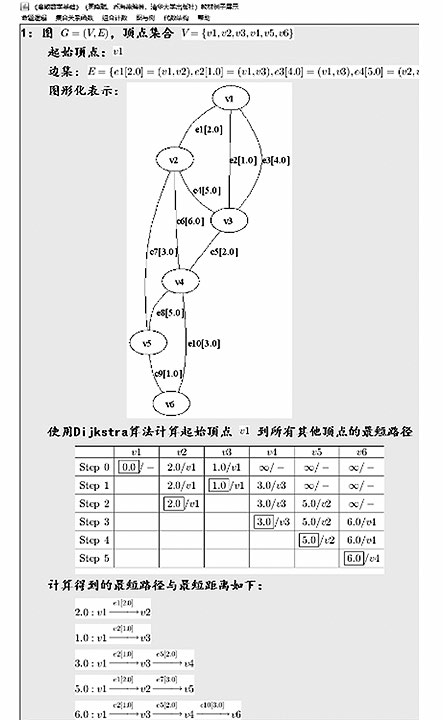
图8 Dijkstra算法求解过程展示
Fig.8 Demonstration of the solution process of Dijkstra algorithm

(3)如何展示一些复杂问题的求解过程，特别是图论模块中最短路径、最小生成树和Huffman树构造算法的求解过程。展示问题求解过程是Deedm软件的重要功能之一，为此我们在实现复杂算法，例如Dijkstra算法、Kruskal算法、Prim算法和Huffman算法的类中设计相应的记录执行算法步骤的类，例如实现带权图实体的类WeightedGraph有内部类DijkstraAlgorithmRecorder，这个类维持一个内部类DijkstraAlgorithmStepRecorder的对象实例列表。类WeightedGraph实现Dijkstra算法的Java方法的主循环将每一次循环产生的关键信息记录在内部类DijkstraAlgorithmStepRecorder的一个对象实例，并添加到DijkstraAlgorithmRecorder的列表中。上层程序在调用实现Dijkstra算法后可获得一个DijkstraAlgorithmRecorder的对象，根据这个对象可展示算法的求解过程。图8给出了Deedm软件基于这个设计使用一个表格展示Dijkstra算法求解过程的效果。这种设计的缺点是当要求解有很多顶点和边的图的最短路径时，DijkstraAlgorithmRecorder对象可能占用很多存储；优点是容易扩充，例如甚至可以设计动画展示DijkstraAlgorithmRecorder存储的信息，实现Dijkstra算法的动画演示效果。

5 结论(Conclusion)

离散数学课程内容比较抽象，教师和学生都需要更多的例子展示离散数学问题的求解过程。我们开发了一款离散数学习题演示软件Deedm，采用面向对象设计，实现了许多离散数学问题的例子生成和求解过程展示。针对中山大学2020 级计算机专业大类一个班68 人的调查表明，虽然没有在课堂上推荐学生下载该软件，这个班仍有19 人从课程的超星在线网站下载并运行了该软件，这19 人中有6 人表示该软件对离散数学课程作业的完成非常有帮助，有11 人表示该软件有帮助。

需要指出的是，Deedm软件不仅可生成例子和展示求解过程以帮助学生学习，也可以帮助教师在课堂测验和考试出卷时生成例子和答案，从而减轻教师的备课和出卷工作量。教师还可以Deedm软件为基础，开展离散数学课程的一些实验，例如让学生自己编写程序实现离散数学问题的求解并与Deedm软件的结果进行比较，甚至在Deedm软件的基础上进行功能的扩展等。下一步我们也会对Deedm软件的例子生成算法、图论中图形的展示等做进一步优化。

参考文献(References)

[1] 谭作文.离散数学课程中实验教学探讨[J].计算机教育,2010(17):106-109.

[2] Rosen K H.Discrete mathematics and its applications[M].7th ed.New York:The McGraw-Hill Companies,2012:113.

[3] 周晓聪,乔海燕.离散数学基础[M].北京:清华大学出版社,2021:80.

[4] 姜楠,李宣廷,袁刚.离散数学实验教学系统设计[J].大学数学,2019(2):50-54.

[5] 李华昱,张千.离散数学实验平台构建及实验方法研究[J].科教导刊(下旬),2015(30):49-50,52.

[6] 邹乐,华珊珊,吕刚.基于MFC的《离散数学》实验演示系统的设计与实现[J].安徽广播电视大学学报,2013(3):121-124.

[7] 曹晓东,史哲文.离散数学及算法[M].北京:机械工业出版社,2013:192-248.

[8] 吴修国.离散数学基础及实用算法[M].北京:清华大学出版社,2009:61-70.

[9] 周晓聪,乔海燕.面向思维能力培养的离散数学课程教学研究[J].计算机教育,2015(15):27-30.

[10] 谭火彬.UML 2面向对象分析与设计[M].2版.北京:清华大学出版社,2019:9-50.