具有饱和发生率的网络蠕虫病毒模型分析

近年来,随着生活水平的提高,手机、电脑等移动设备也日益普及.这些移动设备在为生活带来便利的同时,也遭受着网络蠕虫病毒的攻击,恶意蠕虫病毒的快速传播对网络安全造成了严重威胁．

准确地分析蠕虫病毒在移动网络中的动态行为已经成为一个值得关注的研究课题,许多研究人员提出了不同的数学模型[1-4].文献[1-2]考虑了隔离策略(即切断感染设备与其他设备的连接),文献[3-4]考虑了接种疫苗策略(即安装有效的杀毒软件),这两种策略都有利于降低蠕虫病毒对移动设备的攻击程度.对网络蠕虫病毒模型的研究表明,发生率在病毒传播方面起着决定作用.随着易感设备或感染设备数量的增加,发生率趋于饱和水平,在这种情况下,双线性发生率[5-6]似乎是不合理的.因此,本文考虑了饱和发生率[7-8],其系统模型为:

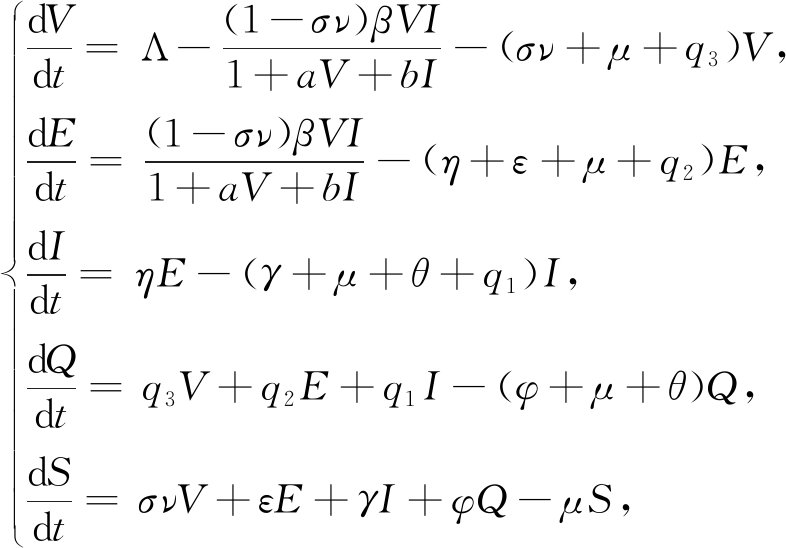
(1)

其中,V(t),E(t),I(t),Q(t),S(t)分别表示在t时刻处于易感状态,潜伏状态,感染状态,隔离状态,安全状态的设备的数量;Λ表示外部设备连入网络的速率;μ表示自然淘汰率;θ表示因病毒入侵所导致的淘汰率;σ表示杀毒软件的有效率;ν表示杀毒软件安装的覆盖率;β代表感染设备对易感设备的传染率;a为预防效果系数;b为治疗效果系表示没有抗病毒性的设备的饱和发生率;η表示从E到I的转移率;ε表示从E到S的转移率;γ表示从I到S的转移率;q3,q2,q1分别表示V,E,I的隔离率;φ表示从Q到S的转移率．

设N(t)为t时刻移动设备的总数,它满足N(t)=V(t)+E(t)+I(t)+Q(t)+S(t).将系统(1)中的方程相加得下面,本文在闭集

Ω=

中研究系统(1)．

1 平衡点和基本再生数

集合Ω是系统(1)的正不变集.通过计算可知系统(1)的无病平衡点:

P0=(V0,E0,I0,Q0,S0)=

(2)

利用下一代矩阵法,计算基本再生数R0的表达式[10]如下:

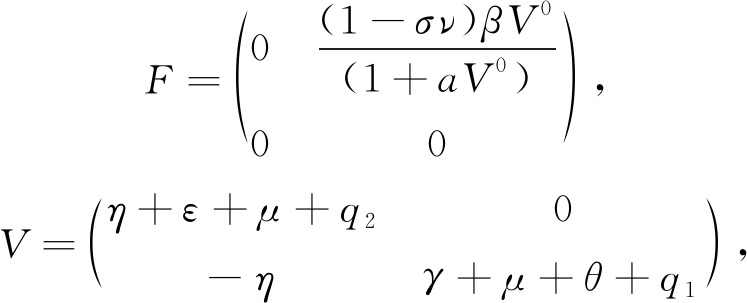
R0=ρ(FV-1)=

(3)

定理1 当R0>1时,系统(1)在Ω内存在唯一的地方病平衡点P*=(V*,E*,I*,Q*,S*)．

证明 令系统(1)的方程右端均等于0,可得

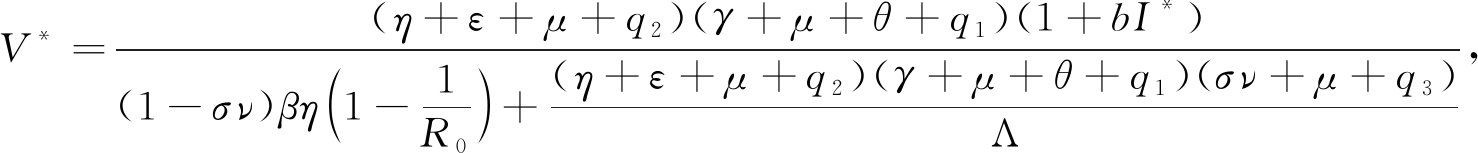
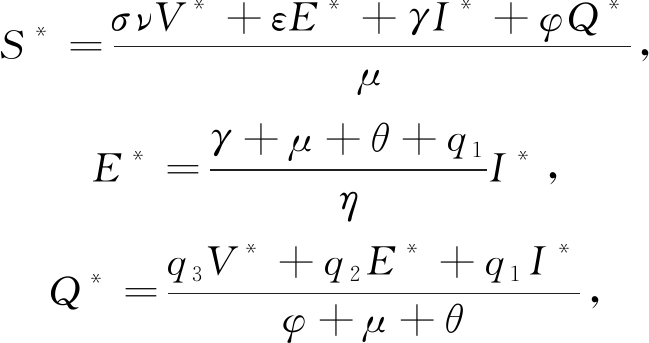
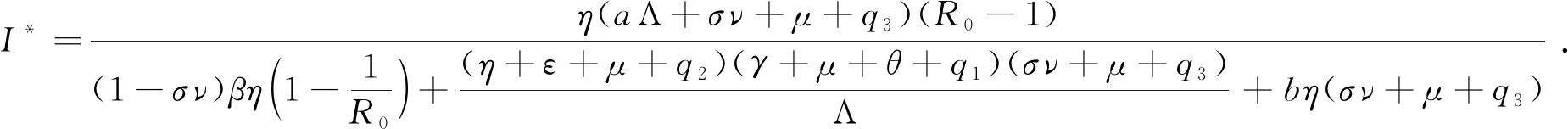
因此当R0>1时,V*,I*>0,定理1得证．

2 平衡点的稳定性

定理2 当R0<1时,系统(1)的无病平衡点P0在Ω内是局部渐近稳定的;当R0>1时,无病平衡点P0是不稳定的．

证明 系统(1)在无病平衡点P0处的Jacobian矩阵为:

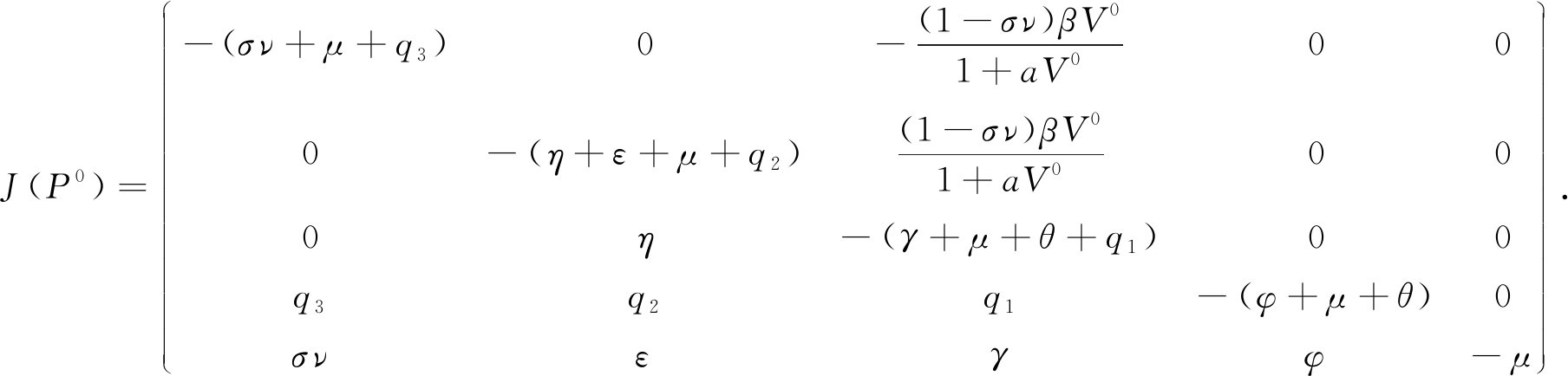
令Φ1(λ)为J(P0)的特征方程,则有

Φ1(λ)=(λ+μ)(λ+φ+μ+θ)·

(4)

解得J(P0)的特征值为λ1=-μ<0,λ2=-(φ+μ+θ)<0,λ3=-(σν+μ+q3)<0和下面方程的根:

λ2+a1λ+a2=0.

(5)

其中,

a1=2μ+η+ε+q2+γ+θ+q1>0,

a2=(η+ε+μ+q2)(γ+μ+θ+q1)-

(η+ε+μ+q2)(γ+μ+θ+q1)(1-R0)．

当R0<1时,a1,a2>0,a1a2>0.根据Hurwitz判据[11],方程(4)的所有根的实部均为负,平衡点P0局部渐近稳定.当R0>1时,a2<0,即方程(4)有根具有正实部,平衡点P0不稳定．

定理3 当R0<1时,系统(1)的无病平衡点P0在Ω内是全局渐近稳定的．

证明 构造Lyapunov函数

L(t)=ηE+(η+ε+μ+q2)I.

(6)

计算L(t)沿着系统(1)的导数得:

(η+ε+μ+q2)(γ+μ+θ+q1)(R0-1)I,

所以当R0<1时,有当且仅当I=0.因此,当R0<1时,的最大不变集为

P0=(V0,E0,I0,Q0,S0)=

根据LaSalle不变集原理[12]可知,当R0<1时,定理3成立．

定理4 当R0>1时,地方病平衡点P*在Ω内是局部渐近稳定的．

证明 系统(1)在地方病平衡点P*处的Jacobian矩阵为:

J(P*)=

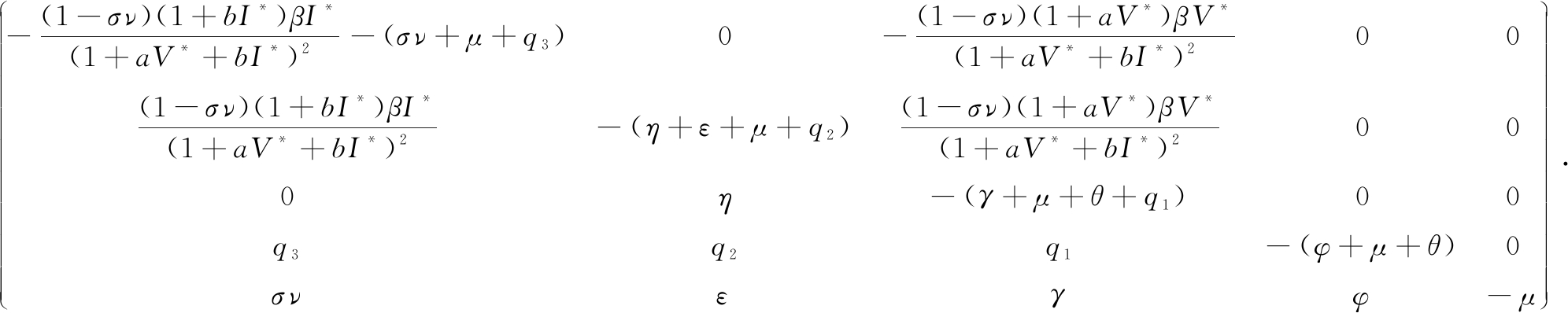
令Φ2(λ)为J(P*)的特征方程,则有

Φ2(λ)=(λ+μ)(λ+φ+μ+θ)·

(λ3+b1λ2+b2λ+b3)=0.

(7)

解得J(P*)的特征值为:λ1=-μ<0,λ2=-(φ+μ+θ)<0和下面方程的根:

λ3+b1λ2+b2λ+b3=0.

(8)

其中,

b1=+σν+3μ+q3+

η+ε+q2+γ+θ+q1,

b2=

(η+ε+μ+q2)+

(γ+μ+θ+q1)+

(η+ε+μ+q2)(γ+μ+θ+q1)-

,

b3=

(η+ε+μ+q2)(γ+μ+θ+q1)-

当R0>1时,有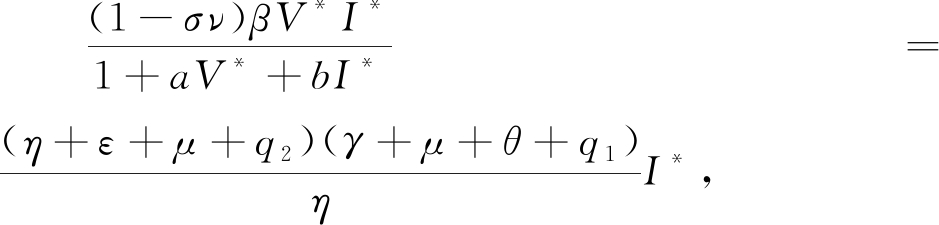通过计算可知

b1,b2,b3>0,Δ1=b1>0,

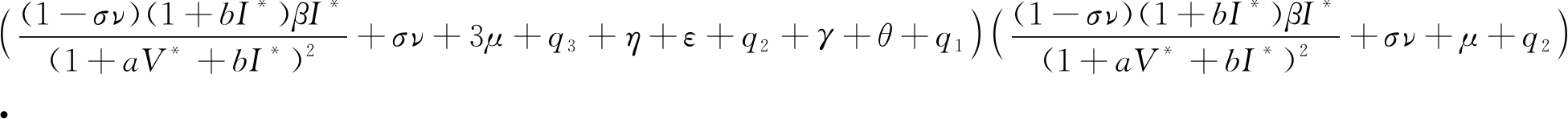
根据Hurwitz判据[11],R0>1时,方程(7)的所有根都具有负实部,定理4得证．

定理5 当R0>1时,地方病平衡点P*在Ω内是全局渐近稳定的．

证明 利用Li-Muldowney几何方法[13]来证明.显然系统(1)满足Ω是单连通的且存在一个紧的吸引集K⊂Ω[14].通过上述论证可知,当R0>1时,无病平衡点P0∈∂Ω是不稳定的,而唯一的正平衡点P*∈Ω是局部渐近稳定的.下面仅需证明q<0即可．

首先,考虑系统(1)的子系统

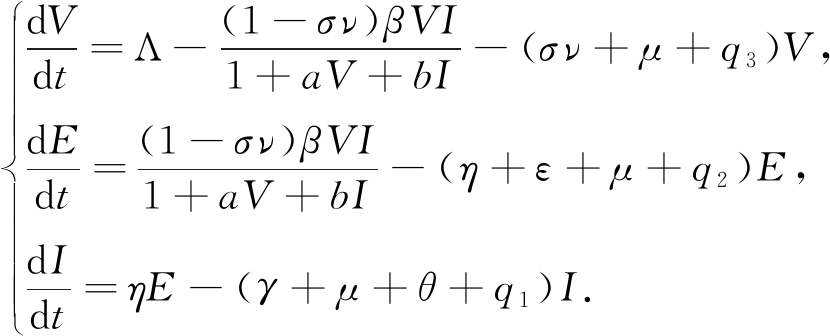
(9)

系统(9)的Jacobian矩阵为

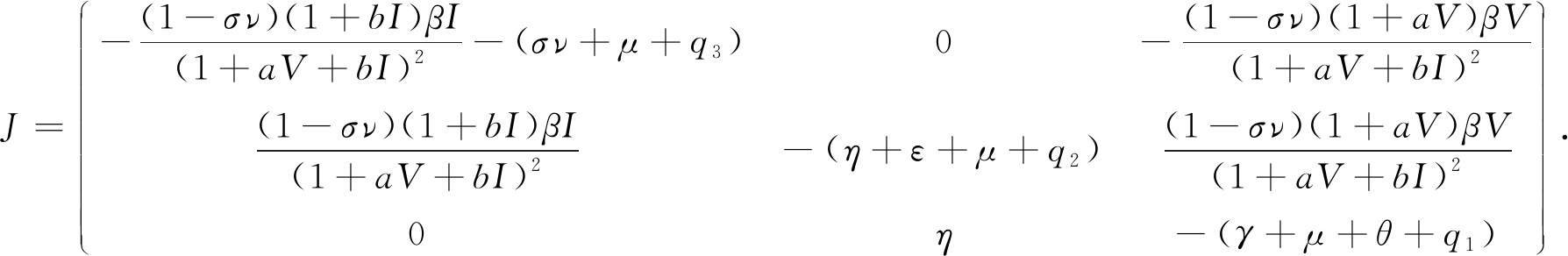
其第二加性复合矩阵为

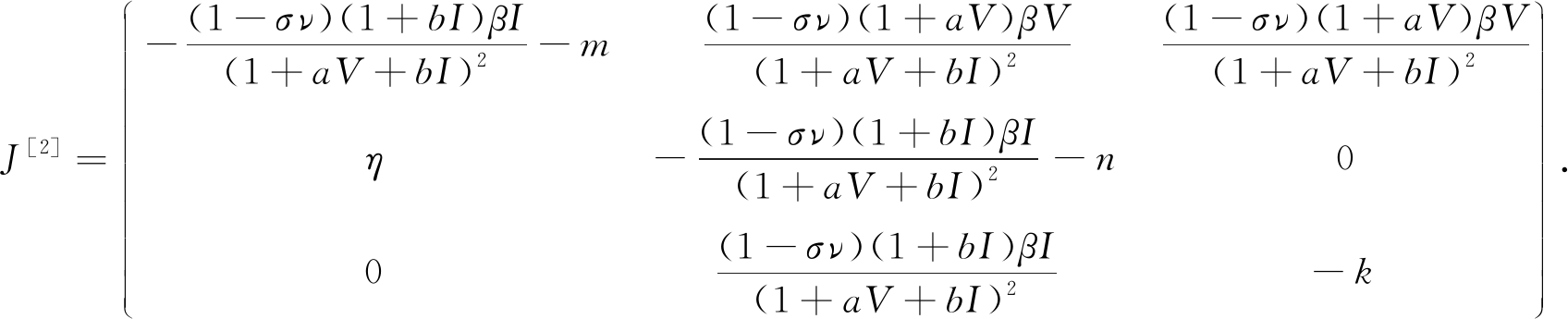
其中,m=σν+2μ+q3+η+ε+q2,n=σν+2μ+q3+γ+θ+q1,k=η+ε+2μ+q2+γ+θ+q1．

令则从而

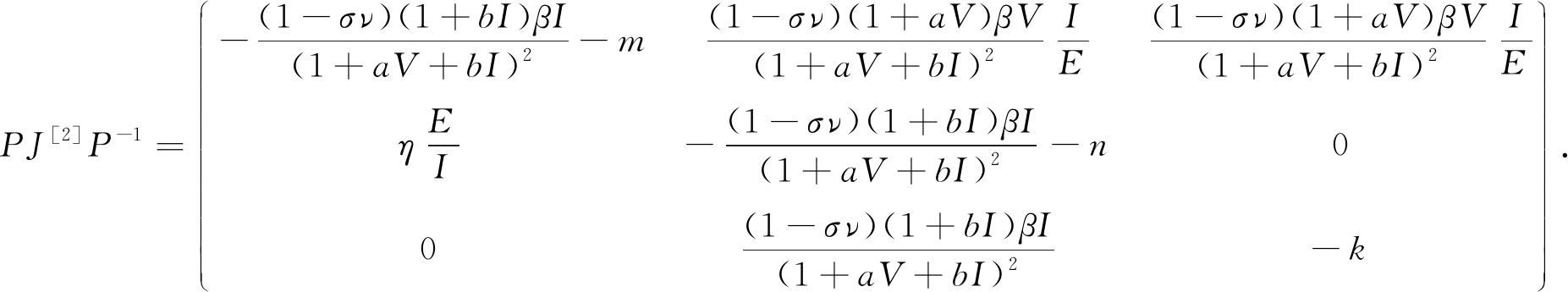
矩阵B=PfP-1+PJ[2]P-1可以写成矩阵形式:其中

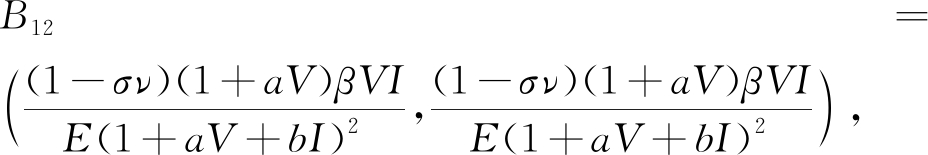
B22=

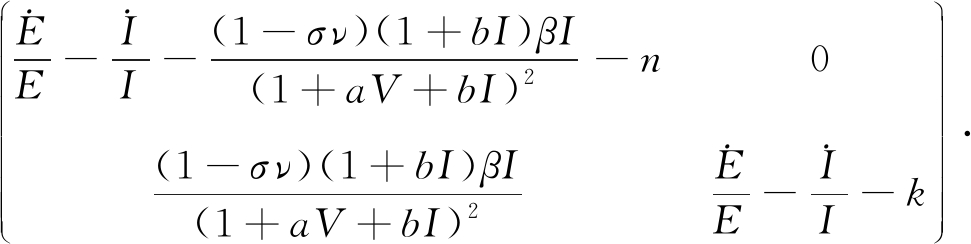
设(u,ν,ω)为R3中的一个向量,其范数定义为相应于范数的Lozinskil测度是μ(B).利用文献[15]的估值方法得μ(B)≤sup{g1,g2},其中g1=μ1(B11)+|B12|,g2=|B21|+μ1(B22).|B12|,|B21|是相应于l1向量范数的矩阵范数,μ1是相应于l1范数的Lozinskil测度.

且

因此,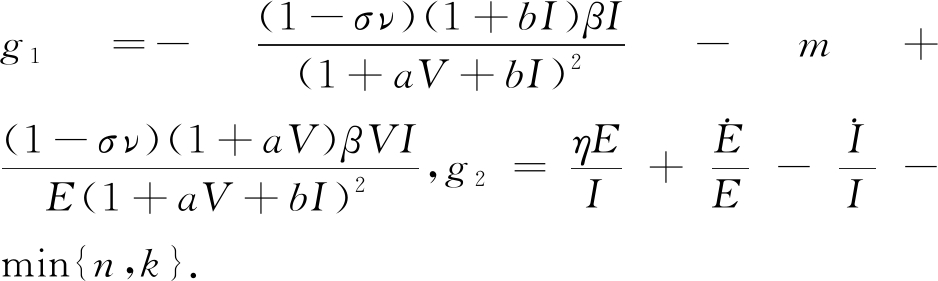由(1)可知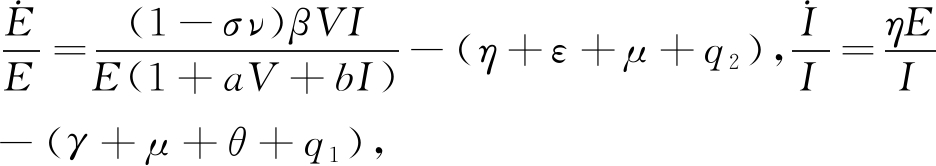所以

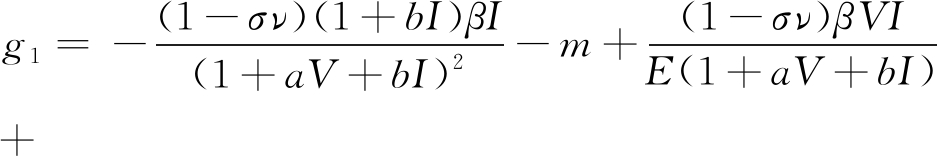
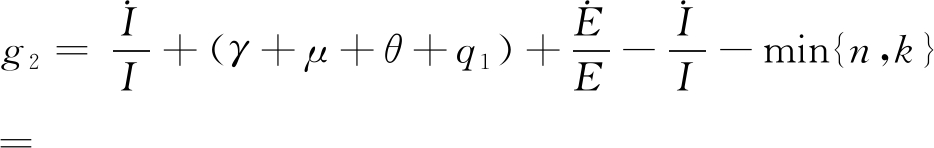
因此可得:

μ(B)≤sup{g1,g2}≤

则即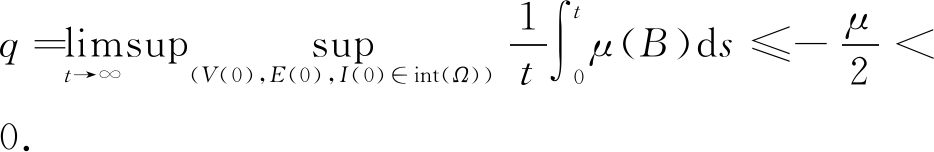

根据文献[4]的定理6,系统(1)的地方病平衡点(V*,E*,I*)是全局渐近稳定的．

现在考虑系统(1)的子系统

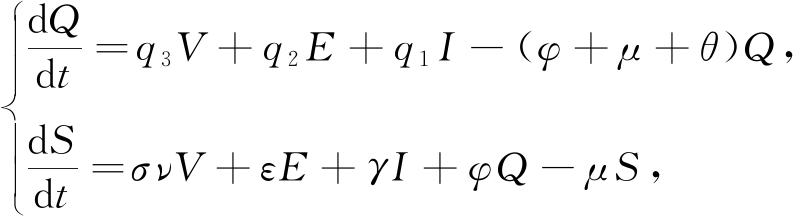
(10)

其极限系统为

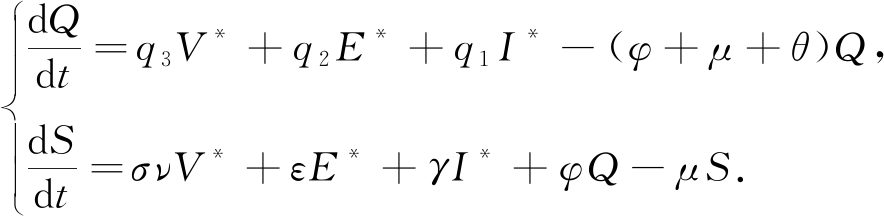
(11)

然后,根据(11)可得

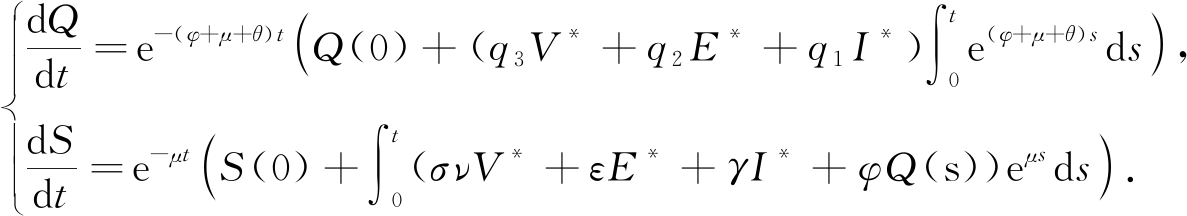
由文献[8]的定理2.5可知,当t→∞时, 且故定理5得证．

3 数值模拟和敏感性分析

利用MATLAB验证无病平衡点P0、地方病平衡点P*的稳定性,选择相同的初值(V(0),E(0),I(0),Q(0),S(0))=(50000,25000,25000,0,0)．

图1:取参数Λ=0.82,σ=0.63,ν=0.5,a=0.045,b=0.76,η=0.0082,β=0.046,γ=0.05,φ=0.0005,μ=0.000011,ε=0.0008,θ=0.0013,q1=0.01,q2=0.0023,q3=0.0014.此时R0≈0.8647<1,满足定理3的条件.图1(a)中显示了五种状态的移动设备的数量随时间的变化规律.安全设备S(t)的数量先增加后趋于稳定,隔离设备Q(t)的数量达到峰值后减小,易感设备V(t),潜伏设备E(t)和感染设备I(t)的数量随时间t急剧下降.由图1(b)可知,t趋于无穷时,易感设备V(t)和隔离设备Q(t)的数量达到一个稳定数值,但潜伏设备E(t)和感染设备I(t)为零,意味着病毒传播结束,与定理3的结论一致.

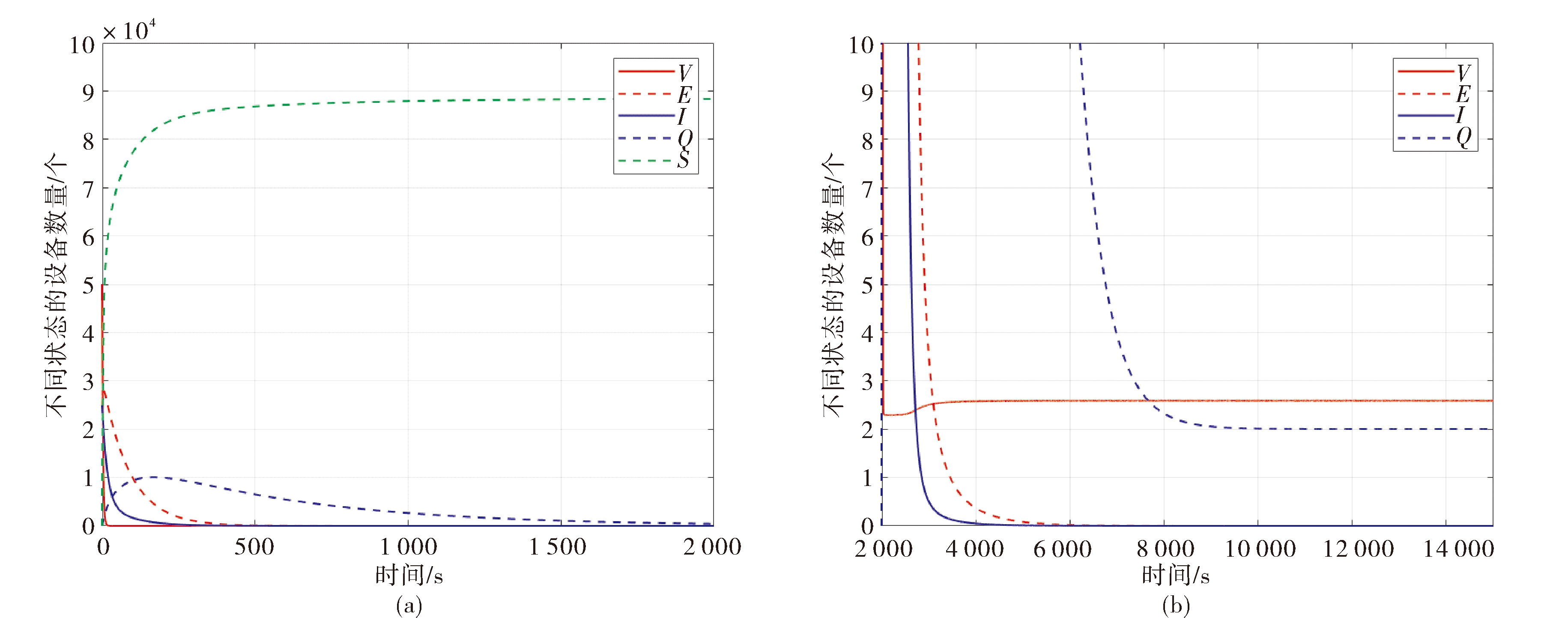
图1 无病平衡点的稳定性
Fig.1 Stability of disease-free equilibrium

图2:取参数ν=0.1,其余参数和图1的参数一样.此时R0≈4.1250>1,满足定理5的条件.对比图1(a)和图2(a)知,两图中五种状态的移动设备的数量随时间t变化的总体趋势一致.但当t趋于无穷时,通过图2(b)知道,易感设备V(t),隔离设备Q(t),潜伏设备E(t)和感染设备I(t)的数量都大于零,表明病毒仍然存在,移动设备将持续受到蠕虫病毒的攻击,与定理5的结论吻合．

基本再生数R0和其他参数的关系见图3.其中σ,ν,ε,γ,q1,q2,q3与R0呈负相关,Λ,β,η与R0呈正相关,并且σ,ν,q1的变化对R0更敏感.结果表明,增大感染设备的隔离率q1,增大杀毒软件安装的覆盖率ν及有效率σ都可以使基本再生数R0减小,即减少感染设备与其他设备的连接,以及提高人们对有效抗病毒软件的认识,都可以达到控制蠕虫病毒传播的效果．

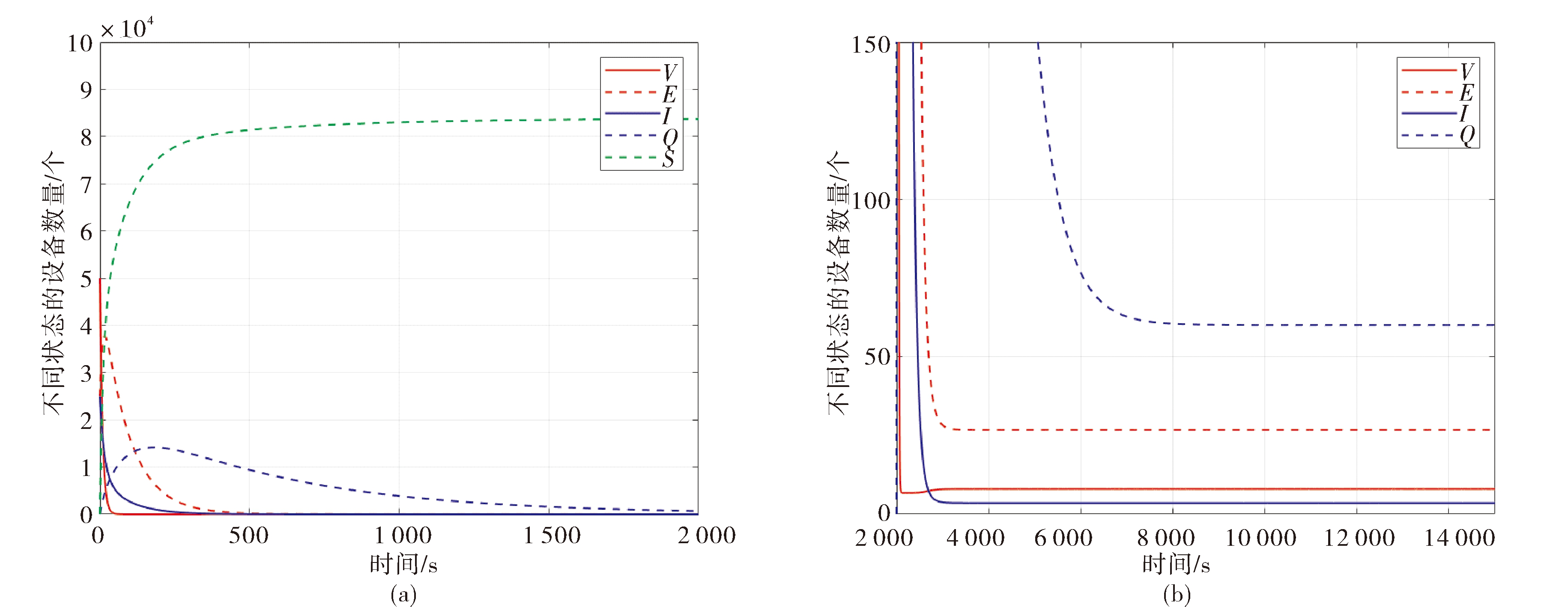
图2 地方病平衡点的稳定性
Fig.2 Stability of endemic equilibrium

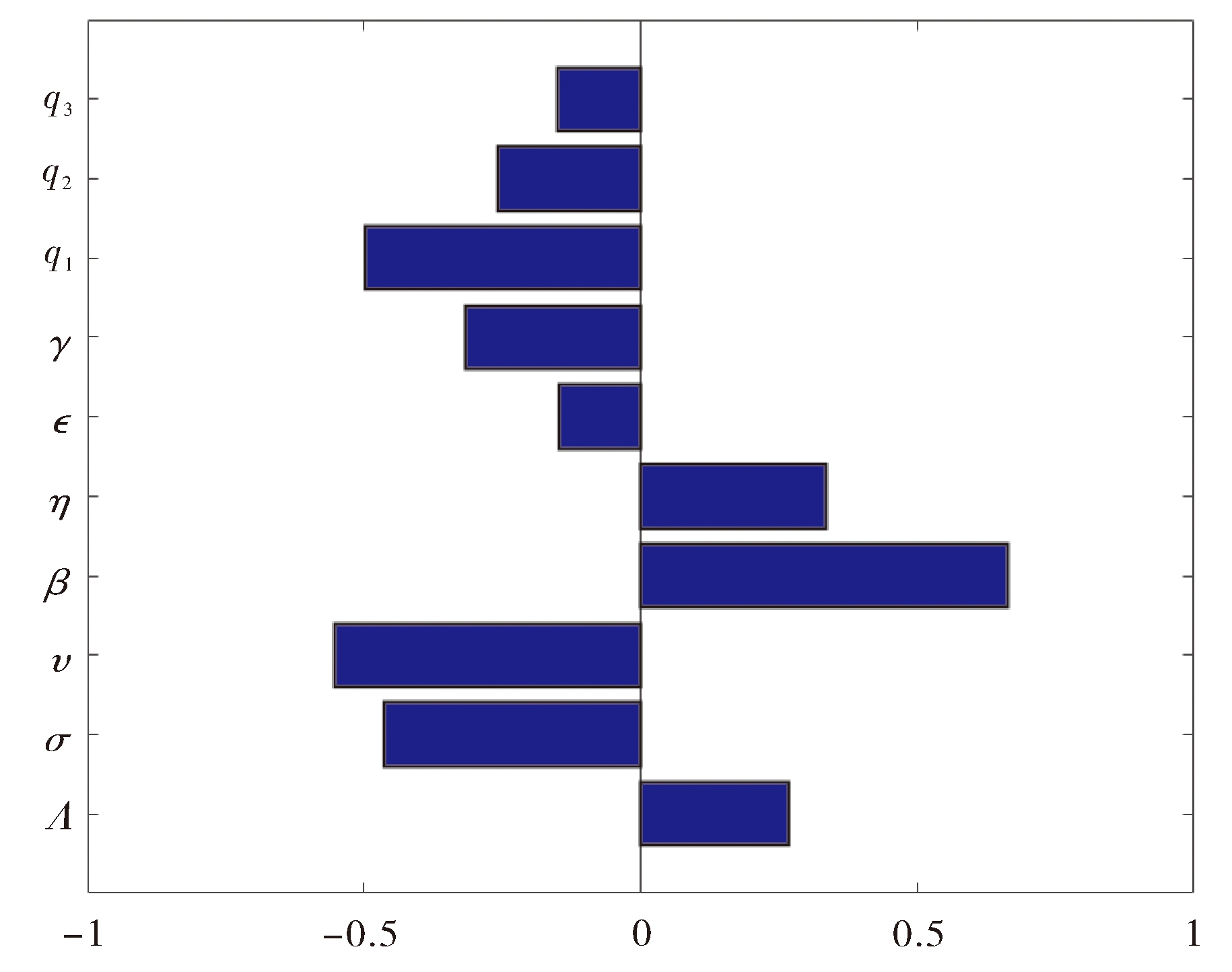
图3 R0与参数的相关性
Fig.3 Correlation between R0 and parameters

4 结论

本文讨论了采用疫苗接种和隔离控制策略的具有饱和发病率的网络蠕虫病毒的VEIQS模型的稳定性.通过分析得到以下结论:1)基本再生数R0对蠕虫病毒传播与否起着决定性的作用,当R0<1时,蠕虫病毒传播结束;当R0>1时,蠕虫病毒仍在网络中传播,并通过数值模拟进行了验证.2)移动设备的隔离率以及人们对有效抗病毒软件的认识直接影响着基本再生数R0大小,可以通过加大参数q1,ν和σ的值来减小R0,从而实现对蠕虫病毒传播的控制．

参考文献：

[1] BADSHAH Q. Global stability of SEIQRS computer virus propagation model with non-linear incidence function[J]. Applied Mathematics, 2015, 6(11): 1926-1938．

[2] XIAO X, FU P, DOU C S, et al. Design and analysis of SEIQR worm propagation model in mobile internet[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 43: 341-350．

[3] KIM K S, IBRAHIM M M, JUNG H, et al. Mathematical analysis of the effectiveness of control strategies to prevent the autorun virus transmission propagation[J/OL]. Applied Mathematics and Computation, 2020, 371(C)[2022-03-17].https:doi.org/10.1016/j.amc.2019.124955.

[4] GAO Q W, ZHUANG J. Stability analysis and control strategies for worm attack in mobile networks via a VEIQS propagation model[J/OL]. Applied Mathematics and Computation, 2020, 368(C)[2022-03-17].https://doi.org/10.1016/j.amc.2019.124584.

[5] 陈中祥. 一类潜伏期与传染期均传染的SEIQR传染病模型[J]. 数学理论与应用, 2010, 30(2): 23-29．

CHEN Z X. A kind of SEIQR epidemical model with infectious force in the latent period and infected period[J]. Mathematical Theory and Applications, 2010, 30(2): 23-29.(Ch)．

[6] 孙雅楠, 薛亚奎, 孙 松. 受疾病意识影响的SIR传染病模型分析[J]. 华中师范大学学报(自然科学版), 2021, 55(3): 337-342．

SUN Y N, XUE Y K, SUN S. Analysis of an SIRS epidemic model with the effects of disease awareness[J]. Journal of Central China Normal University (Natural Sciences), 2021, 55(3): 337-342. (Ch)．

[7] CRUZ V D L, ALBERTO D. Global stability of infectious disease models with contact rate as a function of prevalence index[J]. Mathematical Biosciences and Engineering: MBE, 2017, 14(4): 1019-1033.

[8] LIU X B, YANG L J. Stability analysis of an SEIQV epidemic model with saturated incidence rate[J]. Nonlinear Analysis: Real World Applications, 2012, 13(6): 2671-2679．

[9] DUBEY B, DUBEY P, DUBEY U S. Dynamics of an SIR model with nonlinear incidence and treatment rate[J]. Applications and Applied Mathematics, 2015, 10(2): 718-737．

[10] DRIESSCHE P V D, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1-2): 29-48．

[11] 王拉娣. 传染病动力学模型及控制策略研究[D]. 上海:上海大学, 2005.

WANG L D. Research on the epidemic models and controlling strategy of epidemic dieases[D]. Shanghai: Shanghai University, 2005. (Ch)．

[12] LA SALLE J P. The stability of dynamical systems[C]//Regional Conference Series in Applied Mathematics.Philadelphia:SIAM,1976.

[13] IMRAN M, USMAN M, MALIK T, et al. Mathematical analysis of the role of hospitalization/isolation in controlling the spread of Zika fever[J]. Virus Research, 2018, 255: 95-104．

[14] BUTLER G, WALTMAN P, FREEDMAN H I. Uniformly persistent systems[J]. Proceedings of the American Mathematical Society, 1986, 96(3): 425-430．

[15] MARTIN R H. Logarithmic norms and projections applied to linear differential systems[J]. Journal of Mathematical Analysis and Applications, 1974, 45(2): 432-454．